I hear and I forget. I see and I remember. I do and I understand.
~Confucius
I implemented a (very) simple agent to optimally play the game of tic tac toe (or noughts and crosses). In this post, I will outline the algorithm I used, how I modelled the problem, and walk you through the code. Feel free to mess around with the code here. It is surprising how the core search algorithm is just around 20 lines of code.
Motivation
Well, I am self-learning the AI course offered by my university which is taught by an exceptional professor. It is rare that I find myself wanting to code every algorithm taught in class let alone show up to class. I guess I am just too choosy when it comes to learning1. Anyhow, I decided to implement the minimax algorithm to solve tic-tac-toe because it seems fun, tractable, and a good way to brush up recursion programming. I spent around 1.5 hours coding and an hour debugging the whole thing (with some help from dear ChatGPT).
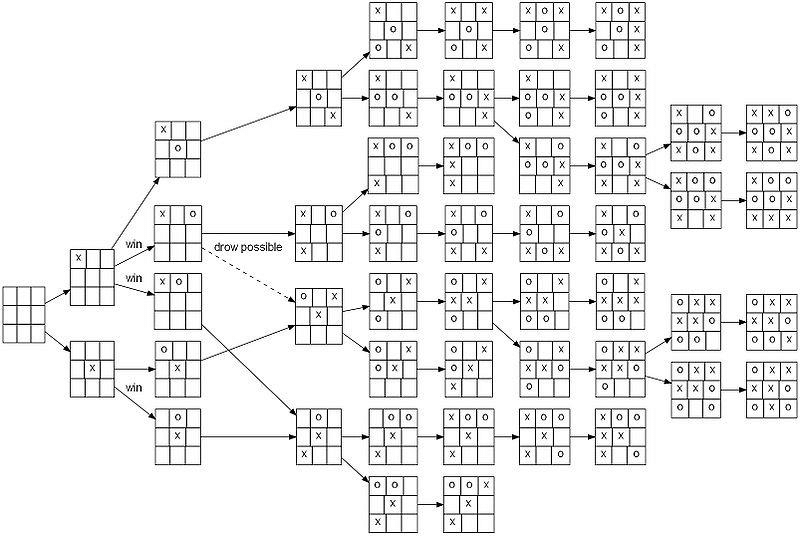
A typical Tic Tac Toe game tree
Tic Tac Toe for dummies
This section is probably preposterous but for the sake of completeness, here is how tic-tac-toe is played. It is a 2-player turn based game where each player places their piece “X” or “O” on a 3x3 grid. The first player to make a horizontal, vertical, or diagonal combination wins. It is what is called a deterministic, two-player, zero sum, fully observable game in game theory parlance. These kinds of games can be optimally solved theoretically and can be solved in practice if you just throw enough compute at some naive algorithm. One such naive but foundational algorithm is minimax.
What is the minimax algorithm?
The core abstraction that we will work with is called a game tree. It is an abstract object which formalizes all possible ways that a game can proceed. We represent game states as nodes of this tree and represent reachable game states as children based on some valid move. Of course, some states are better than others from the player’s perspective. How can we formalise this idea? We assign values to each node in the game tree representing how good it is to be in that state. This is convenient because it allows us to apply utility maximization to compute best moves. A little thought will convince you that if you can compute all possible ways a game can be played and pick the best moves based on utility maximization, you have indeed found the optimal game play. Nobody can beat you.
How do we compute these node values? Assume we are thinking from the computer’s perspective. We need to output a move from the available set of moves given the game state. If I give you the value of the game state if you played one of the moves, you can tell me the best move (just pick the move with the max value). We recursively construct this tree implicitly in the code by counterfactually reasoning about “what if? scenarios” - “What if X played at position 3, then O can play at positions 5, 6, 7. But if it plays at 6 then X wins, so it must play at 5 to block X” and similar arguments.
This should give you an idea about the adversarial nature of minimax. The values for the computers are exactly the opposite of the values for the human. If we looked at the game trees constructed by the two players from a given game state, they would be exactly same except that all the values would be inversed. The minimax algorithm formalises this notion by maximizing values for its own actions and minimizing values for the opponent’s actions. We’ll see how it’s implemented in code later. The big assumption here is that your opponent is also a rational agent trying to maximise its own utility.
Modelling TicTacToe as Adversarial search
What do we really need to make this agent? Well, we need to represent the game state somehow. This is implemented as a simple 9 element list of strings in Python where “-” represents an empty cell.
game: list[“X” | “O” | “-”]
We need a function to decide whether we have a winner. This is implemented by the get_winner(game) function which is really just a dumb bunch of if-elses due to the simple and small number of win conditions for TicTacToe.
def get_winner(self):
# verticals
if self.game[0] == "X" and self.game[3] == "X" and self.game[6] == "X":
return "X"
elif self.game[1] == "X" and self.game[4] == "X" and self.game[7] == "X":
return "X"
elif self.game[2] == "X" and self.game[5] == "X" and self.game[8] == "X":
return "X"
# horizontals
elif self.game[0] == "X" and self.game[1] == "X" and self.game[2] == "X":
return "X"
elif self.game[3] == "X" and self.game[4] == "X" and self.game[5] == "X":
return "X"
elif self.game[6] == "X" and self.game[7] == "X" and self.game[8] == "X":
return "X"
# diagonals
elif self.game[0] == "X" and self.game[4] == "X" and self.game[8] == "X":
return "X"
elif self.game[2] == "X" and self.game[4] == "X" and self.game[6] == "X":
return "X"We need functions which can transition the game state, namely game.make_move(position, piece) and its inverse game.undo_move(position). Simple and cute functions.
def make_move(self, pos, piece):
if self.game[pos] != "-":
raise ValueError("Uh oh, cannot make move, cell already occupied!")
self.game[pos] = piece
def undo_move(self, pos):
self.game[pos] = "-"
We also need a function which will allow us to evaluate how good a board state is. How can we do this? Well, assume if there are no more moves left, what can happen now? It’s either a draw or we have a winner. Accordingly, we can return 0, 1 (if the computer wins) or -1 (if the human wins). That’s for the leaves, you say, but what about the non-leaf nodes? Well, we simply recurse on the children on the current node and return the best value (minimizing or maximising based on the level parity which represents whose turn it is).
Implementation details and caveats
I’ll not go through every line of code but I’ll note some interesting caveats and bugs I came across while implementing this. There’s one obvious limitation in the code. It doesn’t let you choose your piece. The human is always “X” and always the first to move. Maybe one of you can raise a PR!
Initially, I was always checking for the termination condition for the recursion when there were no available moves left which meant at level 9 but I realised that games can also end at the higher level. That’s when I modified the agent’s compute_move function to check for wins or losses just after it makes a counterfactual move. If it does, then we can just return and save ourselves from recursing!
def compute_node_value(self, level):
"""
Assumption, we are at max nodes on odd numbered levels
we are on min nodes on even numbered levels
Output: (val, pos)
"""
moves = self.agentgame.get_available_moves()
# pdb.set_trace()
if len(moves) == 0:
self.max_depth = level
self.nodes_explored += 1
return (self.evaluate_board_state(self.agentgame), -1) # at the leaf, there are no valid moves as there are no children of leaf
values = []
self.total_branches += len(moves)
for move in moves:
self.agentgame.make_move(move, "O" if level % 2 == 1 else "X")
self.nodes_explored += 1
if self.agentgame.get_winner() in ("X", "O"):
values.append((self.evaluate_board_state(self.agentgame), move))
else:
val, _ = self.compute_node_value(level + 1)
values.append((val, move))
self.agentgame.undo_move(move)
if level % 2 == 1: # odd valued levels are max levels
return max(values, key=lambda x: x[0])
else: # even valued levels are min levels
return min(values, key=lambda x: x[0])
One more subtle bug which ChatGPT helped me identify was the value function was computing the values and moves of the current node but was somehow returning the moves of the children. Well, you can never be too careful in recursion hell.
Even after reading the code again and again, I still found that the agent was playing stupidly. I suspected that this was due to my stupidity (!) which indeed, it was. I was calling the agent at each game state with an incremental level value which essentially turned it into its own adversary and it was flipping between it’s own friend and foe. LOL.
Results and demo run
I also felt like collecting some statistics to see how large the search trees were. On my laptop, search was instantaneous and the maximum nodes explored were around 60K at the start of the game. The search tree drastically reduces with each level as the number of valid moves decreases.
==== AGENT COMPUTATION SUMMARY ====
Making move 0 with value 0
Max depth explored: 9
Nodes explored: 60112
Total branches: 55504
Average branching factor: 0.9233430928932659
===== END AGENT COMPUTATION SUMMARY ====
Here’s a simplified game run. I chose this because the computer actually beat me as I wasn’t paying attention and it forced me into a game state to guarantee its win. Bewildering stuff!
❯ python tictactoe.py
Move number: 1
- - -
- - -
- - -
Enter move> 1
==== AGENT COMPUTATION SUMMARY ====
Making move 0 with value 0
Max depth explored: 9
Nodes explored: 69088
Total branches: 63904
Average branching factor: 0.9249652616952293
===== END AGENT COMPUTATION SUMMARY ====
Move number: 2
O X -
- - -
- - -
Enter move> 2
==== AGENT COMPUTATION SUMMARY ====
Making move 3 with value 1
Max depth explored: 7
Nodes explored: 1336
Total branches: 1228
Average branching factor: 0.9191616766467066
===== END AGENT COMPUTATION SUMMARY ====
Move number: 3
O X X
O - -
- - -
Enter move> 6
==== AGENT COMPUTATION SUMMARY ====
Making move 4 with value 1
Max depth explored: 7
Nodes explored: 44
Total branches: 44
Average branching factor: 1.0
===== END AGENT COMPUTATION SUMMARY ====
Move number: 4
O X X
O O -
X - -
Enter move> 5
==== AGENT COMPUTATION SUMMARY ====
Making move 8 with value 1
Max depth explored: 7
Nodes explored: 3
Total branches: 3
Average branching factor: 1.0
===== END AGENT COMPUTATION SUMMARY ====
Oops, better luck next time!
O X X
O O X
X - O
Further improvements
There are so many improvements you can try out. TicTacToe with minimax is like the baseline launchpad to explore adversarial games.
Alpha-beta pruning is an obvious optimization although its advantage cannot be felt with such a small game tree (relative to laptop performance).
You can try to look at stochastic games and implement expectiminimax. Or try one of the many Tic Tac Toe variants.
If you’re feeling ambitious, you can model a completely different game like Poker or Backgammon and implement your own agent.
References
- COL333 course Prof Mausam IIT Delhi
- AIMA Russell et. al. 4th edition Chapter 6 (Adversarial Search)
Footnotes:
- Which is a good thing! To actively resist spending time on useless learning is an optimal strategy to acquire most useful knowledge.
Basil | @itbwtsh
Tech, Science, Design, Economics, Finance, and Books.
Basil blogs about complex topics in simple words.
This blog is his passion project.